Blockchain

MERKLE TREES

Introduction

(For a better experience, we recommend looking at this page in a laptop or desktop)

Let's begin with a simple concept: One-way hashing functions.

A one-way hashing function is a simple mechanism that takes in something as an input and produces a unique hash value for it. The hashing function we will be using is called SHA-256.

Let's try it. Input some text into the box below and click the "Hash It!" button.

Hash It!

Whatever text you hashed, should always produce the same result. For instance, you can go to this website and enter the same text you entered in the "Hash It" box and you should get the same output.

This presents a very interesting possibility. Could I also do this with a file? The answer is "Yes". You can put a file through a hashing function and get a hash value. Then, other people can verify the contents of the file by downloading the file and using the same hashing function to produce a hash value. Let's see an example.

Imagine you have a simple zip archive with 4 files in it. The achive is on the web somewhere. You need to download it and make sure that the file downloaded correctly. In other words, you have to verify that the archive you have is the same as the one that was uploaded to the web site.

The archive contains the following files:

• blockFunctions.js
• consensus.html
• index.html
• merkle.html

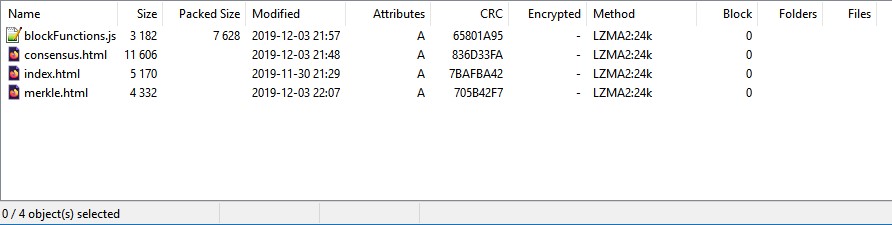
By using a hashing utility such as CRC SHA, which usually comes installed with 7-zip, we can hash the contents of the whole zip archive and get a result.

By clicking on the * simbol, we can get all the resulting hashes.

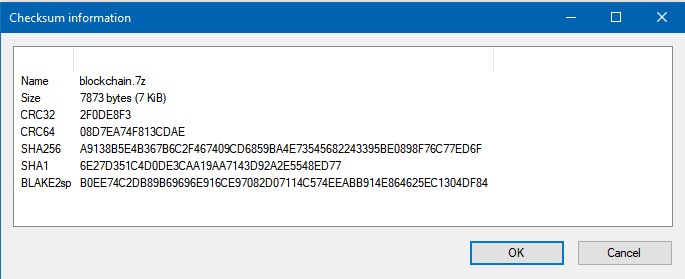
If you go to the repo page, you can download this zip file and hash it. You should get the same results as shown on the image above.

Merkle Trees Explained

Now that you are familiar with hashing, let's look at how it fits in with merkle trees.

A merkle tree is a data structure that is made out of hashes. Merkle trees are based on binary search trees. But each node in the tree is a hash of it's two child nodes.

Typically, the leaf nodes at the bottom of the tree, are the hash of something real. That means the leaf nodes of the tree usually represent actual files. In our prior example, we could hash each file individually and then use the merkle tree algorithm to build the tree.

Once the merkle tree is built, the top hash is called the merkle root. The merkle root is a representation of a whole unit.

In Bitcoin's merkle tree algorithm, each leaf node is the hash of a transaction. A transaction is a record of an exchange of bitcoins between different parties. Each transaction is hashed using the SHA-256 algorithm. This process is similar to how we can use the CRC SHA utility to hash a zip archive.

But Bitcoin's algorithm uses a SHA-256 double hash. Fancy term, it just means that you hash something and then you hash the hash. Confused? Let's try it. Remember our hash it box? We'll use it again. Enter something in the text box and then hash it.

Hash It!

Delete your original text from the box. Then, copy the resulting hash value and paste in the box. Click Hash It! again.

Let's see a real example. Block 150000 in the Bitcoin blockchain has the following transactions hashes (also known as IDs):

• bcdc61cbecf6137eec5c8ad4047fcdc36710e77e404b17378a33ae605920afe1
• f7f4c281ee20ab8d1b00734b92b60582b922211a7e470accd147c6d70c9714a3
• b5f6e3b217fa7f6d58081b5d2a9a6607eebd889ed2c470191b2a45e0dcb98eb0
• 4206f171f06913b1d40597edcaf75780559231fb504c49ba85a4a9ae949e8b95
• a1a6ad6ff321c76496a89b6a4eb9bcfb76b9e068b677d5c7d427c51ca08c273d
• 89c82039452c14a9314b5834e5d2b9241b1fdccdb6e4f4f68e49015540faaf95
• 25c6a1f8c0b5be2bee1e8dd3478b4ec8f54bbc3742eaf90bfb5afd46cf217ad9
• 57eef4da5edacc1247e71d3a93ed2ccaae69c302612e414f98abf8db0b671eae
• 8d30eb0f3e65b8d8a9f26f6f73fc5aafa5c0372f9bb38aa38dd4c9dd1933e090
• 13e3167d46334600b59a5aa286dd02147ac33e64bfc2e188e1f0c0a442182584

You can verify this by going to Block Operations. Enter 150000 in the Height text box and click the "Get Block By Height" button.

These hashes are the result of hashing all the information in a transaction to come up with a unique fixed-length value that identifies the transaction with respect to the entire blockchain.

Bitcoin's algorithm takes pairs of hash values and hashes them together to come up with a new hash value. If the number of hash values is odd at any given level of the tree, the last hash is hashed with itself. This simple process is repeated until reaching the top of the tree. At that point, the last resulting hash is the Merkle Root.

Below is a break down of how the process takes place.

Go to Top